Research Symposium

BIO

Hello, my name is Christopher Cliadakis. I am second-year studying Applied Mathematics and Finance. I am currently researching Physics-Informed Neural Networks (PINNs) and their use as a numerical method for solving real-world problems. After completing my undergraduate studies, I plan to pursue a master's degree in applied mathematics, with an interest in numerical analysis and dynamical systems.

Physics-Informed Neural Networks: A Deep Learning Framework for Solving Differential Equations

Abstract

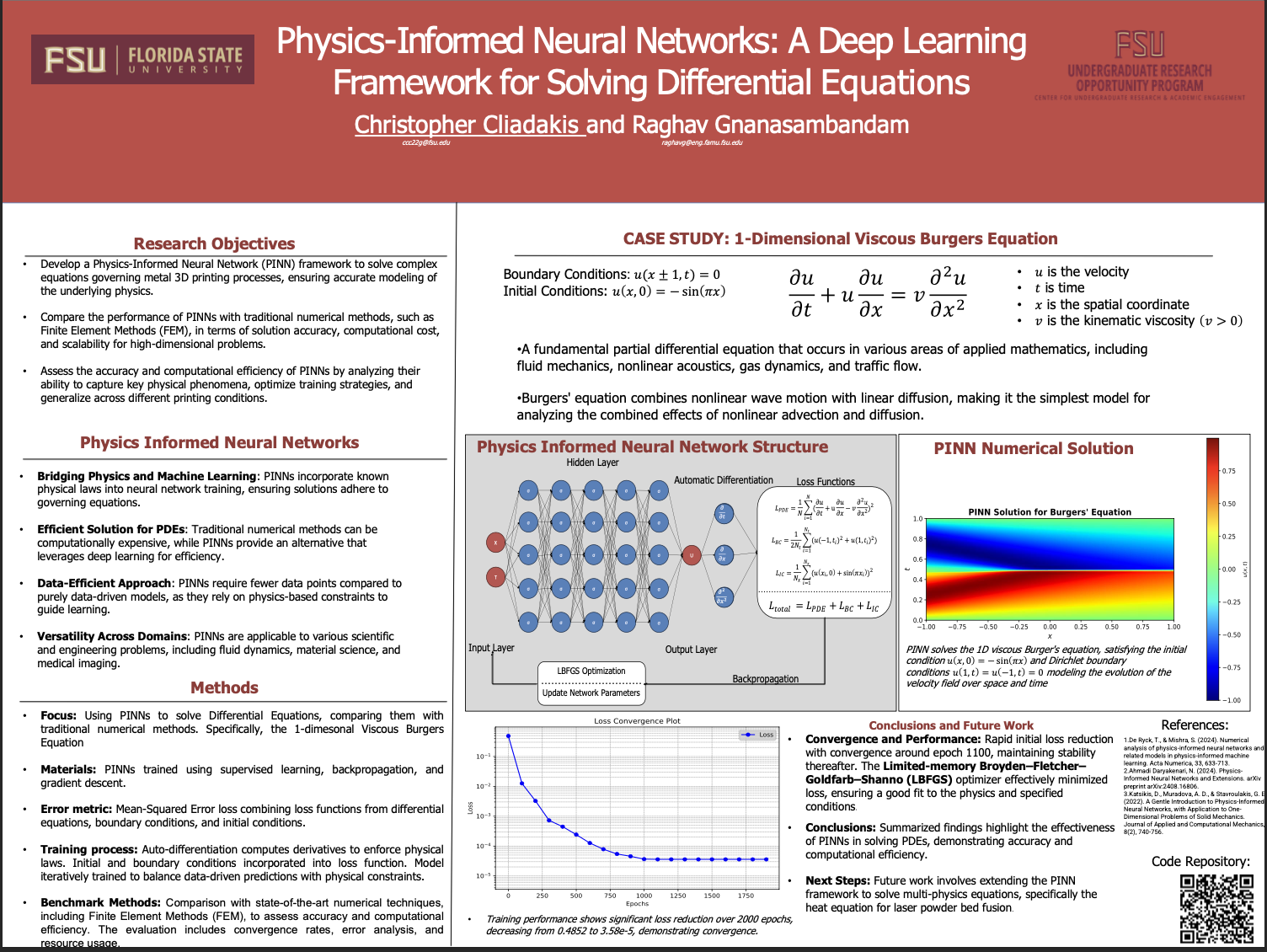
Solving Partial Differential Equations (PDEs) is a fundamental challenge in scientific computing, with applications spanning physics, engineering, and finance. Traditional numerical methods, such as finite difference and finite element methods, can be computationally expensive and struggle with high-dimensional problems. This research confirms the effectiveness of Physics-Informed Neural Networks (PINNs) as an alternative approach to generating numerical solutions for PDEs. By integrating physics-based constraints into neural network training, PINNs offer a data-efficient way to approximate solutions while maintaining accuracy.
To evaluate the performance of PINNs, a neural network model was developed and trained to solve the 1-dimensional viscous burgers equation . The accuracy of the PINN was assessed by comparing its numerical solutions to those obtained from traditional methods. The primary evaluation metrics included the number of training epochs required for convergence and the Mean Squared Error (MSE) loss, with a target threshold of 1e-4. Data collection focused on tracking model convergence and computational efficiency.
The results confirm that PINNs can approximate solutions to PDEs with competitive accuracy while potentially reducing computational complexity. These findings demonstrate the feasibility of PINNs as an alternative to conventional numerical methods, particularly in scenarios where data is limited or high-dimensional solutions are required.
This study provides valuable insights into applying deep learning techniques to numerical analysis and contributes to ongoing advancements in scientific computing.

Keywords: Machine Learning, Numerical Methods, Scientific Computing